Misc

Misc#

check_type()#

check_type(x, what='str')[source]#

Check type of input

Creates a list of boolean values to check if the input is of the target type.

Parameters:

x (int, list, pd.DataFrame, pd.Series, np.ndarray) – Target of checking
what (str) – Compare the dtype of target with what.

Returns:

array – An array of boolean values.

Examples

In [1]: import neurokit2 as nk

In [2]: nk.check_type([1, 2, 3, "hello"], what="str")
Out[2]: array([False, False, False,  True])

In [3]: nk.check_type(pd.DataFrame({"A": [3, 1, 2, 4, 6, np.nan],
   ...:                             "B": [3, 1, 2, "hello", 6, 5]}), what="str")
   ...: 
Out[3]: array([False,  True])

expspace()#

expspace(start, stop, num=50, out=<class 'int'>, base=1)[source]#

Exponential range

Creates a list of integer values (by default) of a given length from start to stop, spread by an exponential function.

Parameters:

start (int) – Minimum range values.
stop (int) – Maximum range values.
num (int) – Number of samples to generate. Default is 50. Must be non-negative.
out (type) – Type of the returned values. Default is int.
base (float) – If 1, will use np.exp(), if 2 will use np.exp2().

Returns:

array – An array of integer values spread by the exponential function.

Examples

In [1]: import neurokit2 as nk

In [2]: nk.expspace(start=4, stop=100, num=10)
Out[2]: array([  4,   6,   9,  13,  18,  26,  36,  51,  71, 100])

In [3]: nk.expspace(start=0, stop=1, num=10, out=float)
Out[3]: 
array([0.        , 0.08005974, 0.16652904, 0.25992105, 0.36079   ,
       0.46973449, 0.58740105, 0.71448797, 0.85174942, 1.        ])

find_closest()#

find_closest(closest_to, list_to_search_in, direction='both', strictly=False, return_index=False)[source]#

Find the closest number in the array from a given number x

Parameters:

closest_to (float) – The target number(s) to find the closest of.
list_to_search_in (list) – The list of values to look in.
direction (str) – "both" for smaller or greater, "greater" for only greater numbers and "smaller" for the closest smaller.
strictly (bool) – False for strictly superior or inferior or True for including equal.
return_index (bool) – If True, will return the index of the closest value in the list.

Returns:

closest (int) – The closest number in the array.

Example

In [1]: import neurokit2 as nk

# Single number
In [2]: x = nk.find_closest(1.8, [3, 5, 6, 1, 2])

In [3]: x
Out[3]: 2

In [4]: y = nk.find_closest(1.8, [3, 5, 6, 1, 2], return_index=True)

In [5]: y
Out[5]: 4

# Vectorized version
In [6]: x = nk.find_closest([1.8, 3.6], [3, 5, 6, 1, 2])

In [7]: x
Out[7]: array([2, 3])

find_consecutive()#

find_consecutive(x)[source]#

Find and group consecutive values in a list

Parameters:: x (list) – The list to look in.
Returns:: list – A list of tuples corresponding to groups containing all the consecutive numbers.

Examples

In [1]: import neurokit2 as nk

In [2]: x = [2, 3, 4, 5, 12, 13, 14, 15, 16, 17, 20]

In [3]: nk.find_consecutive(x)
Out[3]: [(2, 3, 4, 5), (12, 13, 14, 15, 16, 17), (20,)]

find_groups()#

find_groups(x)[source]#

Find and group repeating (identical) values in a list

Parameters:: x (list) – The list to look in.
Returns:: list – A list of tuples corresponding to groups containing all the consecutive numbers.

Examples

In [1]: import neurokit2 as nk

In [2]: x = [2, 2, 2, 2, 1, 3, 3, 2, 2, 2, 1]

In [3]: groups = nk.find_groups(x)

In [4]: groups
Out[4]: [[2, 2, 2, 2], [1], [3, 3], [2, 2, 2], [1]]

find_outliers()#

find_outliers(data, exclude=2, side='both', method='sd', **kwargs)[source]#

Identify outliers (abnormal values)

Extreme values identification using different methods, such as:

sd: Data is standardized, i.e., centered and scaled, and absolute value beyond a certain SD threshold are considered as outliers.
norm: Extreme values identified using theoretical percentiles to identify outliers beyond a certain theoretical percentile (assuming the data comes from a normal distribution). For example, with this method, exclude=0.025 (one-sided) corresponds to the 2.5% lower bound of the normal distribution, which corresponds to approx. -1.96 SD. This method is related to the SD one, but instead of specifying the threshold in SDs, it is specified in percentiles.
percentile: Extreme values identified using percentiles.

Parameters:

data (list or ndarray) – Data array
exclude (int, float) – Amount of outliers to detect (depends on the chosen method).
side (str) – Can be "both", "left" or "right". If exclude=0.05 and side="both" and method="norm", 2.5% of extreme observation of each side will be marked as outliers.
method (str) – Can be “standardize” or “percentile”. The default is “standardize”.
**kwargs (optional) – Other arguments to be passed to standardize().

Returns:

outliers (ndarray) – A boolean vector of with True being the outliers.

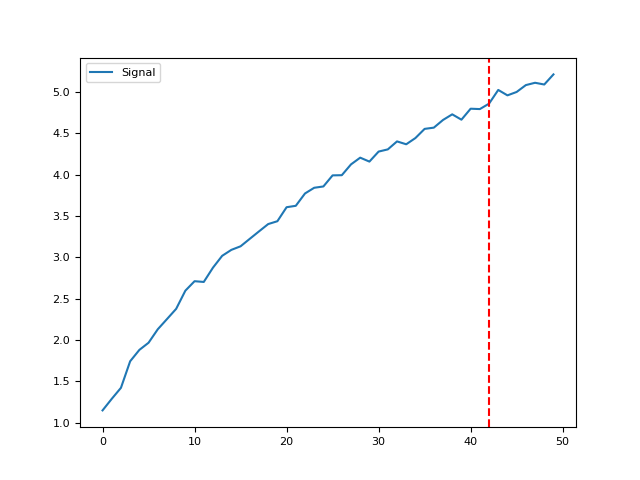
find_plateau()#

find_plateau(values, show=True)[source]#

Find the point of plateau in an array of values

Parameters:

values (ndarray) – An array of values.
show (bool) – If True, will return the plot visualizing the trajectory and point of plateau.

Returns:

plateau (int) – The index of the plateau.

Example

In [1]: import neurokit2 as nk

# Generate values manually
In [2]: x = np.linspace(1, 5, 50)

In [3]: y = 2.5 * np.log(1.3 * x) + 0.5

In [4]: y = y + 0.05 * np.random.normal(size=len(x))

# Find plateau
In [5]: plateau = nk.find_plateau(y, show=True)

In [6]: plateau
Out[6]: 42

find_knee()#

find_knee(y, x=None, S=1, show=False, verbose=True)[source]#

Find Knee / Elbow

Find the knee / elbow in a curve using a basic adaptation of the kneedle algorithm.

Parameters:

x (list) – A vector of values for which to detect the knee / elbow.
S (float) – The sensitivity parameter allows us to adjust how aggressive we want to be when detecting knees. Smaller values detect knees quicker, while larger values are more conservative.

Examples

In [1]: import neurokit2 as nk

In [2]: y = np.log(np.arange(1, 100))

In [3]: y += np.random.normal(0, 0.2, len(y))

In [4]: nk.find_knee(y, show=True)
Out[4]: 21

References

Satopaa, V., Albrecht, J., Irwin, D., & Raghavan, B. (2011, June). Finding a” kneedle” in a haystack: Detecting knee points in system behavior. In 2011 31st international conference on distributed computing systems workshops (pp. 166-171). IEEE.

listify()#

listify(**kwargs)[source]#

Transforms arguments into lists of the same length

Examples

In [1]: import neurokit2 as nk

In [2]: nk.listify(a=3, b=[3, 5], c=[3])
Out[2]: {'a': [3, 3], 'b': [3, 5], 'c': [3, 3]}

parallel_run()#

parallel_run(function, arguments_list, n_jobs=-2, **kwargs)[source]#

Parallel processing utility function (requires the `joblib package)

Parameters:

function (function) – A callable function.
arguments_list (list) – A list of dictionaries. The function will iterate through this list and pass each dictionary inside as **kwargs to the main function.
n_jobs (int) – Number of cores to use. -2 means all but 1. See joblib.Parallel().
**kwargs – Other arguments that can be passed to joblib.Parallel(), such as verbose.

Returns:

list – A list of outputs.

Examples

In [1]: import neurokit2 as nk

In [2]: import time

# The function simply returns the input (but waits 3 seconds.)
In [3]: def my_function(x):
   ...:      time.sleep(3)
   ...:      return x
   ...: 

In [4]: arguments_list = [{"x": 1}, {"x": 2}, {"x": 3}]

In [5]: nk.parallel_run(my_function, arguments_list)
Out[5]: [1, 2, 3]

progress_bar()#

progress_bar(it, prefix='', size=40, verbose=True)[source]#

Progress Bar

Display a progress bar.

Parameters:

it (iterable) – An iterable object.
prefix (str) – A prefix to display before the progress bar.
size (int) – The size of the progress bar.
verbose (bool) – Whether to display the progress bar.

Examples

In [1]: import neurokit2 as nk

In [2]: for i, j in nk.progress_bar(["a", "b", "c"], prefix="Progress: "):
   ...:     pass
   ...: 
Progress: [........................................] 0/3
Progress: [█████████████...........................] 1/3
Progress: [██████████████████████████..............] 2/3
Progress: [████████████████████████████████████████] 3/3


In [3]: print(i, j)
2 c

replace()#

replace(data, replacement_dict)[source]#

Replace values using a dictionary

Parameters:

data (array) – The data to replace values.
replacement_dict (dict) – A replacement dictionary of the form {old_value: new_value}.

Returns:

array – Array containing the replaced values.

Examples

import neurokit2 as nk

data = [0, 1, 2, 3] replacement = {0: 99, 3: 42} replaced = nk.replace(data, replacement) replaced

as_vector()#

as_vector(x)[source]#

Convert to vector

Examples

import neurokit2 as nk

x = nk.as_vector(x=range(3)) y = nk.as_vector(x=[0, 1, 2]) z = nk.as_vector(x=np.array([0, 1, 2])) z

x = nk.as_vector(x=0) x

x = nk.as_vector(x=pd.Series([0, 1, 2])) y = nk.as_vector(x=pd.DataFrame([0, 1, 2])) y

Any function appearing below this point is not explicitly part of the documentation and should be added. Please open an issue if there is one.

Submodule for NeuroKit.

isort:skip_file (since isort-ing the imports generates circular imports)

exception NeuroKitWarning[source]#: Category for runtime warnings that occur within the NeuroKit library.

check_random_state(seed=None)[source]#

Turn seed into a random number generator

Parameters:: seed (None, int, numpy.random.RandomState or numpy.random.Generator) – Seed for the random number generator. If seed is None, a numpy.random.Generator is created with fresh, unpredictable entropy. If seed is an int, a new numpy.random.RandomState instance is created, seeded with seed. If seed is already a Generator or RandomState instance then that instance is used. The manin difference between the legacy RandomState class and the new Generator class is that the former has better reproducibililty and compatibililty guarantees (it is effectively frozen from NumPy v1.16) while the latter has better statistical “randomness” properties and lower computational cost. See: https://numpy.org/doc/stable/reference/random/legacy.html for further information. Note: to initialise the new Generator class with an integer seed, use, e.g.: check_random_state(np.random.SeedSequence(123)).
Returns:: rng (numpy.random.Generator or numpy.random.RandomState) – Random number generator.

check_random_state_children(random_state_parent, random_state_children, n_children=1)[source]#

Create new independent children random number generators to be used in sub-functions

Parameters:

random_state_parent (None, int, numpy.random.RandomState or numpy.random.Generator) – Parent’s random state (see misc.check_random_state).
random_state_children ({‘legacy’, ‘spawn’}, None, int, numpy.random.RandomState or numpy.random.Generator) – If "legacy", use the same random state as the parent (discouraged as it generates dependent random streams). If "spawn", spawn independent children random number generators from the parent random state. If any of the other types, generate independent children random number generators from the random_state_children provided.
n_children (int) – Number of children generators to be spawned.

Returns:

children_generators (list of generators) – List of children random number generators.

copyfunction(func, *args, **kwargs)[source]#: Copy Function

create_report(file='myreport.html', signals=None, info={'sampling_rate': 1000}, fig=None)[source]#

Reports

Create report containing description and figures of processing. This function is meant to be used via the rsp_process() or ppg_process() functions.

Parameters:

file (str) – Name of the file to save the report to. Can also be "text" to simply print the text in the console.
signals (pd.DataFrame) –

A DataFrame of signals. Usually obtained from rsp_process(), ppg_process(), or
emg_process().
info (dict) – A dictionary containing the information of peaks and the signals’ sampling rate. Usually obtained from rsp_process() or ppg_process().
fig (matplotlib.figure.Figure or plotly.graph_objects.Figure) – A figure containing the processed signals. Usually obtained from rsp_plot(), ppg_plot(), or emg_plot().

Returns:

str – The report as a string.

Misc

Contents

Misc#

check_type()#

expspace()#

find_closest()#

find_consecutive()#

find_groups()#

find_outliers()#

find_plateau()#

find_knee()#

listify()#

parallel_run()#

progress_bar()#

replace()#

as_vector()#